NIRVAR: Network Informed Restricted Vector Autoregression

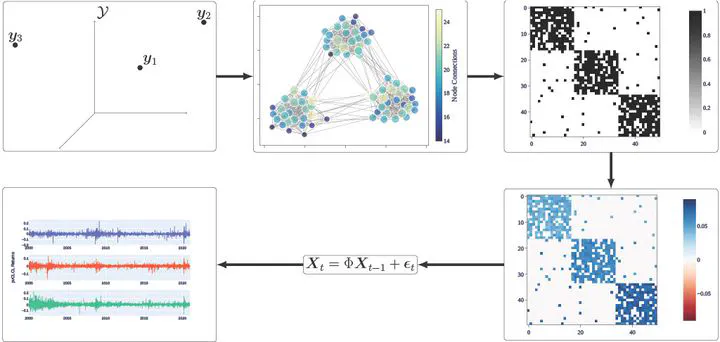
High-dimensional panels of time series arise in many scientific disciplines such as neuroscience, finance, and macroeconomics. Often, co-movements within groups of the panel components occur. Extracting these groupings from the data provides a course-grained description of the complex system in question and can in- form subsequent prediction tasks. We develop a novel methodology to model such a panel as a restricted vector autoregressive process, where the coefficient matrix is the weighted adjacency matrix of a stochastic block model. This network time series model, which we call the Network Informed Restricted Vector Autoregres- sion (NIRVAR) model, yields a coefficient matrix that has a sparse block-diagonal structure. We propose an estimation procedure that embeds each panel component in a low-dimensional latent space and clusters the embedded points to recover the blocks of the coefficient matrix. Crucially, the method allows for network- based time series modelling when the underlying network is unobserved. We derive the bias, consistency and asymptotic normality of the NIRVAR estimator. Simulation studies suggest that the NIRVAR estimated embed- ded points are Gaussian distributed around the ground truth latent positions. On three applications to finance, macroeconomics, and transportation systems, NIRVAR outperforms competing models in terms of prediction and provides interpretable results regarding group recovery.